| HOME | HELP | FEEDBACK | SUBSCRIPTIONS | ARCHIVE | SEARCH | TABLE OF CONTENTS |
|
| ||||||||
![]() Previous
Article | Next
Article
Previous
Article | Next
Article ![]()
The Journal of Neuroscience, December 15, 1998,
18(24):10688-10699 Volen Center for Complex Systems, Brandeis University, Waltham, Massachusetts
02243
A limited number (7 ± 2) of items can be held in human short-term
memory (STM). We have previously suggested that observed dual (theta
and gamma) oscillations could underlie a multiplexing mechanism that
enables a single network to actively store up to seven memories. Here
we have asked whether models of this kind can account for the data on
the Sternberg task, the most quantitative measurements of memory
search available. We have found several variants of the oscillatory
search model that account for the quantitative dependence of the
reaction time distribution on the number of items (S) held in STM.
The models differ on the issues of (1) whether theta frequency varies
with S and (2) whether the phase of ongoing oscillations is reset by
the probe. Using these models the frequencies of dual oscillations
can be derived from psychophysical data. The derived values
(f Key words: theta; gamma; oscillations; working memory; short-term memory;
Sternberg; brain waves The brain has a limited short-term memory (STM) capacity
(7 ± 2 items) for list items, such as the digits in a novel
phone number (Brener, 1940
To further test the concept of a multiplexing buffer, we have asked whether
models of this kind can account quantitatively for data from the
Sternberg task (Sternberg, 1966 In our initial effort to link STM to brain oscillations we pointed out that
the increase in RT with each additional item (the "slope" of the
Sternberg curves) approximates the period of one gamma cycle (Lisman
and Idiart, 1995 A second goal has been to analyze one of the major objections to serial
scanning. A simple exhaustive scanning model would predict that the
RT is the same for all items stored in STM. However, a strong serial
position effect has been found if the retention interval between the
presentation of the list and the probe is <1.5 sec (Clifton and
Birenbaum, 1970 We have sought to find oscillatory models that can account quantitatively for
the details of RT distributions in the Sternberg task. As found by
Sternberg (1966)
The oscillatory models that we have considered are all based on the following
principles: a memory is represented by a subset of neurons firing
within a gamma cycle (Fig. 1). When
multiple memory representations are being kept active during a
retention period, they are activated in successive gamma subcycles of
a theta cycle. This pattern repeats during each theta cycle
(Fig. 4A).
We have previously implemented a physiologically plausible network
model of such a buffer (Lisman and Idiart, 1995
The RT in the Sternberg task can be described as the sum of various
components (Fig. 4A).
In the Sternberg paradigm a probe typically arrives 500-3000 msec
(tretention) after the end of item presentation
(typically 0.5-1.2 sec/item). This probe then has to be identified.
After the item is identified, we assume that there is a wait period
(twait) until the beginning (trough) of a theta
cycle. The probe is then serially compared with the items in the
buffer (scanning) as they are activated (tscan).
Finally, at the next trough the answering process may be initiated
as a motor process of duration tmotor. In the simplest
model, oscillations would be unaffected by presentation of the
probe, and theta frequency would be independent of S. This last
assumption means that even if only two memories are held, there are
five "empty" gamma cycles. In this simple form the model cannot
account for the increase in RT with S, because none of the times
depends on S. Alternatively scanning might be initiated at the
trough of a theta cycle and the motor response delivered at the end
of the last active gamma cycle (not at the trough). In this
model twait does not depend on S but
tscan does. This model can correctly reproduce the
increase in RT with S, because tscan depends on
S. However, it cannot account for the increase in variance with
S, because the only term that depends on S is tscan,
which equals one theta cycle, and this by definition has no variance.
These examples illustrate how models can fail to account for the
detailed data. The next sections describe two models that can account
for the data. The mathematical derivations are given in . Model I: theta frequency depends on the number of memories
being stored (adapting theta model) Figure 4A
describes a model that successfully accounts for the RT data. The theta period
increases with the number of items (S); i.e., the theta frequency
decreases with S. Thus, a key feature of this model is that
there are no "empty" gamma cycles even if the number of stored items
is less than seven. When an additional item is added to STM, the
theta period increases so there is an additional gamma cycle (up to a
limit of seven for digits). Thus a theta period (T
An Oscillatory Short-Term Memory Buffer Model Can Account for Data on the
Sternberg Task
![]()
ABSTRACT
![]() Top
Top ![]() Abstract
Abstract ![]() Introduction
Introduction ![]() Results
Results ![]() Discussion
Discussion ![]() References
References ![]() = 6-10 Hz; f
= 6-10 Hz; f![]() = 45-60 Hz) are in reasonable
agreement with experimental values. The exhaustive nature of the
serial search that has been inferred from psychophysical measurements
can be plausibly explained by these oscillatory models. One argument
against exhaustive serial search has been the existence of serial
position effects. We find that these effects can be explained by
short-term repetition priming in the context of serial scanning
models. Our results strengthen the case for serial processing and
point to experiments that discriminate between variants of the serial
scanning process.
= 45-60 Hz) are in reasonable
agreement with experimental values. The exhaustive nature of the
serial search that has been inferred from psychophysical measurements
can be plausibly explained by these oscillatory models. One argument
against exhaustive serial search has been the existence of serial
position effects. We find that these effects can be explained by
short-term repetition priming in the context of serial scanning
models. Our results strengthen the case for serial processing and
point to experiments that discriminate between variants of the serial
scanning process.
![]()
INTRODUCTION
![]() Top
Top ![]() Abstract
Abstract ![]() Introduction
Introduction ![]() Results
Results ![]() Discussion
Discussion ![]() References
References ![]() ; Miller, 1956
; Miller, 1956![]() ). If human STM is
maintained by active firing as observed in prefrontal cortex of the
monkey (Goldman-Rakic, 1995
). If human STM is
maintained by active firing as observed in prefrontal cortex of the
monkey (Goldman-Rakic, 1995![]() ; Fuster, 1997
; Fuster, 1997![]() ), there is a fundamental
problem of how to keep multiple memories separate. It has been
suggested that this is accomplished by a "buffer" (Atkinson and
Shiffrin, 1968
), there is a fundamental
problem of how to keep multiple memories separate. It has been
suggested that this is accomplished by a "buffer" (Atkinson and
Shiffrin, 1968![]() ), but the physiological
mechanisms that would allow multiple items to be stored in a buffer
are not known. We have proposed (Lisman and Idiart, 1995
), but the physiological
mechanisms that would allow multiple items to be stored in a buffer
are not known. We have proposed (Lisman and Idiart, 1995![]() ; Jensen et al., 1996
; Jensen et al., 1996![]() ) that a single
brain network can separately maintain up to seven memories by a
multiplexing mechanism that uses theta (Gundel and Wilson, 1992
) that a single
brain network can separately maintain up to seven memories by a
multiplexing mechanism that uses theta (Gundel and Wilson, 1992![]() ; Mecklinger
et al., 1992
; Mecklinger
et al., 1992![]() ; Nakamura et al., 1992
; Nakamura et al., 1992![]() ; Iramina et al., 1996
; Iramina et al., 1996![]() ; Krause et
al., 1996
; Krause et
al., 1996![]() ; Sasaki et al., 1996
; Sasaki et al., 1996![]() ; Gevins et al., 1997
; Gevins et al., 1997![]() ; Klimesch et
al., 1997
; Klimesch et
al., 1997![]() ; Tesche, 1997
; Tesche, 1997![]() ) and gamma (Galambos et
al., 1981
) and gamma (Galambos et
al., 1981![]() ; Pantev et
al., 1991
; Pantev et
al., 1991![]() ; Joliot et al., 1994
; Joliot et al., 1994![]() ; Tallon-Baudry et
al., 1997
; Tallon-Baudry et
al., 1997![]() , 1998
, 1998![]() ) brain oscillations for
clocking. A memory is represented by groups of neurons that fire in
the same gamma cycle. Individual memories become serially active in
sequential gamma subcycles of a theta cycle (Fig. 1). This
pattern of activation repeats on subsequent theta cycles. We have
previously shown that a multiplexing buffer of this kind can be
plausibly realized by known biophysical mechanisms (Lisman and
Idiart, 1995
) brain oscillations for
clocking. A memory is represented by groups of neurons that fire in
the same gamma cycle. Individual memories become serially active in
sequential gamma subcycles of a theta cycle (Fig. 1). This
pattern of activation repeats on subsequent theta cycles. We have
previously shown that a multiplexing buffer of this kind can be
plausibly realized by known biophysical mechanisms (Lisman and
Idiart, 1995![]() ; Jensen and Lisman,
1996a
; Jensen and Lisman,
1996a![]() ; Jensen et
al., 1996
; Jensen et
al., 1996![]() ). A key underlying idea
is that a memory is represented by cells firing within a gamma cycle,
and different memory representations are activated in different gamma
cycles. Recent work by Wehr and Laurent (1996)
). A key underlying idea
is that a memory is represented by cells firing within a gamma cycle,
and different memory representations are activated in different gamma
cycles. Recent work by Wehr and Laurent (1996)![]() is consistent with
the idea that gamma oscillations serve as a clock for
information processing. They showed that components of sequences
representing odors are active in successive gamma cycles.
Furthermore, modeling work shows that the phase advance of
hippocampal place cells can be quantitatively explained in terms of
expected positions read out in sequential gamma subcycles of a theta
cycle (Jensen and Lisman, 1996b
is consistent with
the idea that gamma oscillations serve as a clock for
information processing. They showed that components of sequences
representing odors are active in successive gamma cycles.
Furthermore, modeling work shows that the phase advance of
hippocampal place cells can be quantitatively explained in terms of
expected positions read out in sequential gamma subcycles of a theta
cycle (Jensen and Lisman, 1996b![]() ).
).
View larger
version (31K):
[in a new window]
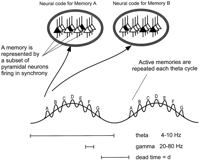
Figure 1. Seven
memories (A-G) are multiplexed; memory A, represented
by a certain spatial pattern of cell firing (oval inset), is
active in the first gamma subcycle of a theta oscillation, followed
by memory B in the next gamma cycle, etc. After a dead time
(d), the seven memories repeat in the subsequent theta cycle.
![]() ). This task
has been extensively used to explore the timing of retrieval from
STM, and there is general agreement about the central findings.
In the task, a list of items is presented rapidly. A few seconds
later, a probe item is presented, and the subject answers as quickly
as possible whether the probe was on the list. A key finding
consistent with serial memory scanning is that the average reaction
time (RT) increases linearly with the number of items on the list
(S). A second key finding is that the increase in RT with S is
the same for "yes" (positive probes) and "no" (negative probes)
answers. This observation led to the suggestion that the search is
exhaustive (Sternberg, 1966
). This task
has been extensively used to explore the timing of retrieval from
STM, and there is general agreement about the central findings.
In the task, a list of items is presented rapidly. A few seconds
later, a probe item is presented, and the subject answers as quickly
as possible whether the probe was on the list. A key finding
consistent with serial memory scanning is that the average reaction
time (RT) increases linearly with the number of items on the list
(S). A second key finding is that the increase in RT with S is
the same for "yes" (positive probes) and "no" (negative probes)
answers. This observation led to the suggestion that the search is
exhaustive (Sternberg, 1966![]() ): the answer can
apparently not be given until the entire list is scanned.
): the answer can
apparently not be given until the entire list is scanned.
![]() ). Furthermore, the
number of gamma subcycles that occur during a theta cycle (Bragin
et al., 1995
). Furthermore, the
number of gamma subcycles that occur during a theta cycle (Bragin
et al., 1995![]() ) is close to the human
memory span of 7 ± 2. It was these correspondences
that suggested that an oscillatory model based on theta and gamma
oscillations might organize STM. However, we did not show that an
oscillatory model could quantitatively explain the full RT
distributions and their dependence on S. This is one of the
goals of the current study.
) is close to the human
memory span of 7 ± 2. It was these correspondences
that suggested that an oscillatory model based on theta and gamma
oscillations might organize STM. However, we did not show that an
oscillatory model could quantitatively explain the full RT
distributions and their dependence on S. This is one of the
goals of the current study. ![]() ; Burrows and Okada,
1971
; Burrows and Okada,
1971![]() ; Forrin and
Cunningham, 1973
; Forrin and
Cunningham, 1973![]() ): subjects respond
faster to items at the end of the list. We have found that this data
can be simply explained by short-term repetition priming in the
context of a serial scanning model.
): subjects respond
faster to items at the end of the list. We have found that this data
can be simply explained by short-term repetition priming in the
context of a serial scanning model.
![]()
RESULTS
![]() Top
Top ![]() Abstract
Abstract ![]() Introduction
Introduction ![]() Results
Results ![]() Discussion
Discussion ![]() References
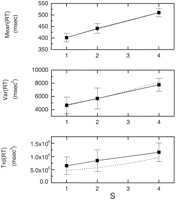
References ![]() , the linear increase in
RT with memory load (S) is ~38 msec/item (Fig. 2). The
increment is the same for negative and positive probes. Sternberg
(1964)
, the linear increase in
RT with memory load (S) is ~38 msec/item (Fig. 2). The
increment is the same for negative and positive probes. Sternberg
(1964)![]() also found
that not only does the RT increase with S, but the variance and
asymmetry (measured by the third central moment) also increase with S
(Fig. 2).
The cumulative RT distributions have been characterized by Ashby et
al. (1993)
also found
that not only does the RT increase with S, but the variance and
asymmetry (measured by the third central moment) also increase with S
(Fig. 2).
The cumulative RT distributions have been characterized by Ashby et
al. (1993)![]() . As seen in Fig.
3,
the cumulative distributions are systematically delayed as S gets
larger. Thus the mean RT increases with S. A final important
feature of the Sternberg data is the effect of serial position:
subjects respond faster to a probe that corresponds to an item
late in the list (Forrin and Cunningham, 1973
. As seen in Fig.
3,
the cumulative distributions are systematically delayed as S gets
larger. Thus the mean RT increases with S. A final important
feature of the Sternberg data is the effect of serial position:
subjects respond faster to a probe that corresponds to an item
late in the list (Forrin and Cunningham, 1973![]() ). However, when
the delay between the presentation of the list and the probe becomes
sufficiently long (>1.5 sec), the serial position effect vanishes
(see Fig. 10).
). However, when
the delay between the presentation of the list and the probe becomes
sufficiently long (>1.5 sec), the serial position effect vanishes
(see Fig. 10).
View larger
version (19K):
[in a new window]
Figure 2. Adapting
theta model fit (dashed lines) to experimental data (solid
lines) for mean, variance, and skewness of the RT distribution
for the Sternberg task. The data obtained by Sternberg are responses
to negative probes only. The best fit using Equations 13,
15,
and 16
resulted in the parameters T ![]() = 22 msec;
pa = 0.88; d = 80.1
msec;
= 22 msec;
pa = 0.88; d = 80.1
msec; ![]() motor = 57 msec; and
t0 = 215 msec. The fit was obtained by
first fitting the slopes of the increases with S and then fitting
motor = 57 msec; and
t0 = 215 msec. The fit was obtained by
first fitting the slopes of the increases with S and then fitting
![]() motor and t0. Error bars
indicate SEs. Data are average of 10 subjects.
motor and t0. Error bars
indicate SEs. Data are average of 10 subjects.
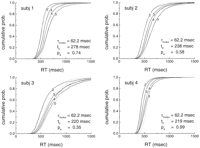
View larger
version (30K):
[in a new window]
Figure 3. Adapting
theta model (dashed lines) fitted to the cumulative RT
distribution for both positive and negative probes (solid
lines) measured by Ashby et al. (1993) ![]() . By applying
a least mean square method the cumulative distributions (Eq. 18)
were fitted. The four values of T
. By applying
a least mean square method the cumulative distributions (Eq. 18)
were fitted. The four values of T![]() are kept
constant across subjects and experiments. For simplicity,
are kept
constant across subjects and experiments. For simplicity, ![]() motor is kept the same for all subjects.
pa and t0 are allowed to vary
individually. Fitted values for T
motor is kept the same for all subjects.
pa and t0 are allowed to vary
individually. Fitted values for T![]() (S = 2, 3, 4, and 5) are
96, 119, 135, and 158 msec, respectively.
(S = 2, 3, 4, and 5) are
96, 119, 135, and 158 msec, respectively. ![]() ; Jensen and
Lisman, 1996a
; Jensen and
Lisman, 1996a![]() ; Jensen et al., 1996
; Jensen et al., 1996![]() ). This model is
constructed of a network of excitatory and inhibitory cells. The
excitatory cells receive an external oscillatory drive at theta
frequency. Each of the excitatory cells have the following
properties: a cell will remain inactive until it is activated by an
external input triggering an action potential. After the action
potential follows a depolarizing ramp (afterdepolarizing potential),
which repeatedly brings the cell to fire in subsequent theta
cycles. This allows the storage of a memory representation by
repeated activation at theta rate. Each time a memory representation
is activated the inhibitory cells in the network provide a
hyperpolarizing feedback. This feedback, which produces the gamma
oscillations, serves to keep multiple memory representation separate
in time. Recurrent collaterals have synaptic weights that encode each
item (but not the unique sequence in the list) and enable the
network to reactivate memories in the correct sequence, even in the
presence of noise.
). This model is
constructed of a network of excitatory and inhibitory cells. The
excitatory cells receive an external oscillatory drive at theta
frequency. Each of the excitatory cells have the following
properties: a cell will remain inactive until it is activated by an
external input triggering an action potential. After the action
potential follows a depolarizing ramp (afterdepolarizing potential),
which repeatedly brings the cell to fire in subsequent theta
cycles. This allows the storage of a memory representation by
repeated activation at theta rate. Each time a memory representation
is activated the inhibitory cells in the network provide a
hyperpolarizing feedback. This feedback, which produces the gamma
oscillations, serves to keep multiple memory representation separate
in time. Recurrent collaterals have synaptic weights that encode each
item (but not the unique sequence in the list) and enable the
network to reactivate memories in the correct sequence, even in the
presence of noise.
View larger
version (20K):
[in a new window]
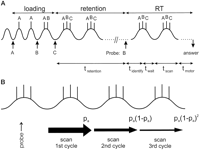
Figure 4. Diagrams
indicating definition of relevant times and the concept of adapting
theta. A, Three items (A-C) are loaded; the theta
period increases by one gamma period as each additional item is
loaded (Eq 1).
After loading, there is a delay period
(tretention) in which the items are maintained by
activity-dependent intrinsic properties of the neurons coding these
items (Lisman and Idiart 1995 ![]() ; Haj-Dahmane
and Andrade, 1997
; Haj-Dahmane
and Andrade, 1997![]() ). After
probe presentation the items can be scanned, i.e., compared with the
probe as they are activated. Scanning must wait until a trough of
the theta cycle is reached, giving rise to a wait time
(twait). After scanning the motor response is
initiated at the first possible trough, contributing to the time,
tmotor. B, There is a high probability,
pa, that the answer will be initiated after the
first complete scan. If not, scanning will be repeated and the
response initiated at the end of the second scan with probability
pa (1
). After
probe presentation the items can be scanned, i.e., compared with the
probe as they are activated. Scanning must wait until a trough of
the theta cycle is reached, giving rise to a wait time
(twait). After scanning the motor response is
initiated at the first possible trough, contributing to the time,
tmotor. B, There is a high probability,
pa, that the answer will be initiated after the
first complete scan. If not, scanning will be repeated and the
response initiated at the end of the second scan with probability
pa (1 ![]() pa). The figure shows the
probability of response after n scans (a geometric
distribution; Eq. 11).
This skipping process is responsible for the increase in skewness
(third moment) of the RT distribution with S.
pa). The figure shows the
probability of response after n scans (a geometric
distribution; Eq. 11).
This skipping process is responsible for the increase in skewness
(third moment) of the RT distribution with S. ![]() )
depends on the number of gamma periods (T
)
depends on the number of gamma periods (T![]() ) per
theta cycle:
) per
theta cycle:
Here
d is a "dead time" denoting the part of the trough of the theta
oscillations where no memories are active (Fig. 1).
Such "theta adaptation" is plausible given the observed frequency
variability of brain theta oscillations: correlations between
memory tasks and oscillations have been observed in the 4-7 Hz
band (Gevins et al., 1997
![]()
(1) ![]() ; Klimesch et al., 1997
; Klimesch et al., 1997![]() ; Sarnthein et
al., 1998
; Sarnthein et
al., 1998![]() ) and also at higher
frequencies (10-12 Hz) (Krause et al., 1996
) and also at higher
frequencies (10-12 Hz) (Krause et al., 1996![]() ). Note that in contrast
to the subsequent model, we assume here that the phase of theta is
not reset by the probe. Because T
). Note that in contrast
to the subsequent model, we assume here that the phase of theta is
not reset by the probe. Because T![]() varies with S, a
wait time, twait, described by a uniform
distribution (Eq. 8), is
introduced. Thus, in this model both mean and variance increase with
S, in accord with the data.
varies with S, a
wait time, twait, described by a uniform
distribution (Eq. 8), is
introduced. Thus, in this model both mean and variance increase with
S, in accord with the data.
The motor response is described by an exponential distribution with a constant offset (Eq. 3), contributing tmotor to the average RT. The motor response gives a constant contribution to the variance of the RT distribution independent of S.
These assumptions alone predict a symmetrical RT distribution, but the
observed distribution is skewed and has a skewness that increases
with S (Fig. 2). To
account for these features, we assumed that the probability of giving
an answer (pa) at the end of a theta cycle is
<1; if no answer is given, scanning is repeated (Fig. 4B).
We term this "skipping." The long RTs produced by skipping will
produce the skewness in the distribution. The longer the theta
period, the longer the duration of a skip. Thus, this effect can
account for the increase in skewness with S (it also adds to the mean
and variance of the RT). From these assumptions the full RT
distribution can be derived (Eq. 17), as
well as the mean, variance, and skewness (Eqs. 13, 15, 16). These
expressions can be fit to the experimental data by finding the best
parameters T![]() , d,
pa,
, d,
pa, ![]() motor, and t0. The constant
t0 determines the offset of the cumulative
distribution and is defined in Equation 7. The
dotted lines in the graphs of Figure 2 are the
best fit of this model and account well for how the average,
variance, and skewness of the RT distribution increase with
S. These data were provided to us by S. Sternberg
(University of Pennsylvania).
motor, and t0. The constant
t0 determines the offset of the cumulative
distribution and is defined in Equation 7. The
dotted lines in the graphs of Figure 2 are the
best fit of this model and account well for how the average,
variance, and skewness of the RT distribution increase with
S. These data were provided to us by S. Sternberg
(University of Pennsylvania).
The model can also be tested against the data of Ashby et al. (1993)![]() , which provides a
complete RT distribution. In Figure 3 we have
replotted the RT distributions from Ashby et al. (1993)
, which provides a
complete RT distribution. In Figure 3 we have
replotted the RT distributions from Ashby et al. (1993)![]() as cumulative
distributions. In fitting the data it was assumed for simplicity that
all subjects have the same theta period (T
as cumulative
distributions. In fitting the data it was assumed for simplicity that
all subjects have the same theta period (T![]() ) for a
given value of S. The free parameters are T
) for a
given value of S. The free parameters are T![]() (S),
which depends on T
(S),
which depends on T![]() and d, and
and d, and
![]() motor, t0, and pa.
The latter two are assumed to be unique for each subject. The derived
cumulative distributions were fit to the data using a procedure that
minimizes the least square error.
motor, t0, and pa.
The latter two are assumed to be unique for each subject. The derived
cumulative distributions were fit to the data using a procedure that
minimizes the least square error.
The cumulative distributions are well fit by the model for all values of S
and for all subjects (Fig. 3). The
derived values of T![]() as a function of S
obtained from the fits are shown in Figure 5. Note that
the increase in theta with S is linear, even though all the theta
values were fit to individual values of S. As S varies, the
theta period varies from 96 to 158 msec (5.8-12.3 Hz).
These numbers are in plausible agreement with observed values in
humans, which show considerable variability [4-7 Hz (Klimesch et al.,
1997
as a function of S
obtained from the fits are shown in Figure 5. Note that
the increase in theta with S is linear, even though all the theta
values were fit to individual values of S. As S varies, the
theta period varies from 96 to 158 msec (5.8-12.3 Hz).
These numbers are in plausible agreement with observed values in
humans, which show considerable variability [4-7 Hz (Klimesch et al.,
1997![]() ), 5.9 Hz (Gevins et
al., 1997
), 5.9 Hz (Gevins et
al., 1997![]() ), 4-7 Hz
(Sarnthein et al., 1998
), 4-7 Hz
(Sarnthein et al., 1998![]() ), 10-12 Hz (Krause et
al., 1996
), 10-12 Hz (Krause et
al., 1996![]() )]. The gamma
period (T
)]. The gamma
period (T![]() ) is the slope of the increase in T
) is the slope of the increase in T![]() with S, and the dead time (d) is the intercept (Fig. 5). The
frequency of gamma derived in this way is 49 Hz, consistent with
typical values of gamma frequency (Galambos et al., 1981
with S, and the dead time (d) is the intercept (Fig. 5). The
frequency of gamma derived in this way is 49 Hz, consistent with
typical values of gamma frequency (Galambos et al., 1981![]() ; Pantev et al.,
1991
; Pantev et al.,
1991![]() ; Joliot et al., 1994
; Joliot et al., 1994![]() ; Singer and Gray, 1995
; Singer and Gray, 1995![]() ; Tallon-Baudry
et al., 1997
; Tallon-Baudry
et al., 1997![]() , 1998
, 1998![]() ). The dead time d
is 75.5 msec.
). The dead time d
is 75.5 msec.
|
Note that we obtained all the fits keeping the theta period at each S (and hence the gamma period) the same for all the subjects. Hence individual differences were accounted for by variation in t0 and pa, both of which are assumed to be independent of S. The variations in t0 might simply reflect individual differences in the rapidity of motor processes. Individual differences in attentiveness might explain variations in pa.
Model II: reset of the slow-wave oscillation
We next asked whether it was possible to find a satisfactory model in which
theta adaptation did not occur. This implies that when the buffer has
fewer items than seven there will be empty "slots" (Fig. 6A).
As stated previously, simple models without theta adaptation do not
work. We have considered the possibility that the phase of ongoing
theta oscillations is "reset" each time a memory set is scanned.
There is evidence for the reset of the theta oscillations in some
brain regions (Berger et al., 1983![]() ; Rahn and
Basar 1993a
; Rahn and
Basar 1993a![]() ,b
,b![]() ; Brankack et al., 1996
; Brankack et al., 1996![]() ; Brandt 1997
; Brandt 1997![]() ). We assume
that the reset is controlled by the external mechanism driving the
network at the theta rhythm. We have further assumed that the reset
does not occur during the part of the theta cycle when the memories
are actively being read out, because this would distort order
information. If the probe identification is completed at a time when
memories are being reactivated at gamma frequency, reset has to wait
(twait) until after activation of the last item
(Fig. 6B,
1). Otherwise the reset occurs immediately (Fig. 6B,
2).
). We assume
that the reset is controlled by the external mechanism driving the
network at the theta rhythm. We have further assumed that the reset
does not occur during the part of the theta cycle when the memories
are actively being read out, because this would distort order
information. If the probe identification is completed at a time when
memories are being reactivated at gamma frequency, reset has to wait
(twait) until after activation of the last item
(Fig. 6B,
1). Otherwise the reset occurs immediately (Fig. 6B,
2).
|
After reset, scanning occurs from the trough to the end of the list (Fig. 6A).
Thus, both twait and tscan depend on
S. This gives rise to an increase in RT with S, which is
approximately linear. It further follows that the wait time (Fig. 6B)
increases with S (Eq. 24). The
random variation in twait accounts for the major
part of the increase in variance of RT with S. As in the
previous model, a skipping process is assumed to account for the
skewness of the distribution. The probability of the answer being
given after the first scan is pa (Fig. 6C).
If for some reason the answer is not given, another scan is initiated
after the theta oscillation has been reset. This produces the
increasing asymmetry of the RT distribution with S (Eq. 25). The
complete expressions for the mean, variance, and asymmetry (third
central moment) are given by Equations 27, 29, and 30, with
the free parameters ![]() motor, t0,
pa, T
motor, t0,
pa, T![]() , and d. The
full RT distribution is given by Equation 31. Note
that the final increase in RT with S has a second-order term
(Eq. 28) because
of the distribution of the wait time. However, for realistic
parameter values, the increase in RT with S is approximately linear.
, and d. The
full RT distribution is given by Equation 31. Note
that the final increase in RT with S has a second-order term
(Eq. 28) because
of the distribution of the wait time. However, for realistic
parameter values, the increase in RT with S is approximately linear.
The three expressions fit quite well to the data of Sternberg (Fig. 7). The fit
is, however, not unique; we can vary the dead time, d (see
Eq. 20), in the
interval from 10 to 100 msec and still obtain fits to the
Sternberg data within the SEs. The resulting values for
f![]() , f
, f![]() , and
pa are shown in Figure 8. Note
that pa and f
, and
pa are shown in Figure 8. Note
that pa and f![]() do not depend
significantly on d, whereas f
do not depend
significantly on d, whereas f![]() does. The
dead time mainly adds to the theta period, but because scanning
occurs from the trough to the end of the list, this does not change
the retrieval properties of the model significantly.
does. The
dead time mainly adds to the theta period, but because scanning
occurs from the trough to the end of the list, this does not change
the retrieval properties of the model significantly.
|
|
As for the previous model, we have derived the expressions for the cumulative
RT distributions to fit the data of Ashby et al. (1993)![]() (Fig. 9). In this
case T
(Fig. 9). In this
case T![]() and
and ![]() motor are kept the same for the four
subjects, and t0 and pa are unique for
each subject. d was fixed to 15 msec and
Sspan = 7.
motor are kept the same for the four
subjects, and t0 and pa are unique for
each subject. d was fixed to 15 msec and
Sspan = 7.
|
We conclude that the reset model accounts for the RT data just as well as the adapting theta model. We are therefore not able to distinguish between the two models on the basis of the psychophysical data only. As will be discussed later, electrophysiological recordings on subjects performing the Sternberg task could be used to distinguish the two models.
Accounting for serial position effect
A major objection to serial scanning has been the existence of serial
position effects: RT is systematically longer for early list items
than late items (Fig. 10,
first panel). Superficially, this is inconsistent with a
scanning process in which each item is handled similarly. An
important hint about the basis of this effect is that it disappears
if the retention interval between list presentation and the probe is
>1.5 sec (Fig. 10). This
suggests that the serial position effect is not fundamental to
scanning itself. For positive items, the probe is a repetition of a
just-presented item, and we propose that the serial position effect
is a consequence of short-term repetition priming (Bertelson and
Renkin, 1966![]() ; Posner and
Keele, 1967
; Posner and
Keele, 1967![]() ; Smith et al., 1973
; Smith et al., 1973![]() ; McKone 1995
; McKone 1995![]() ); the time
needed to identify the probe (tidentify) is decreased if
the item has been presented in the last few seconds. We have assumed
that this priming decays exponentially (
); the time
needed to identify the probe (tidentify) is decreased if
the item has been presented in the last few seconds. We have assumed
that this priming decays exponentially (![]() prime; Eq. 33, Fig. 11).
The time between the presentation of a memory item and the probe
is a function of both the presentation rate, frate, and
the retention interval, tretention. The average
time to identify the probe (tidentify) is
determined by Equation 35. Figure
10 shows
that with a value of
prime; Eq. 33, Fig. 11).
The time between the presentation of a memory item and the probe
is a function of both the presentation rate, frate, and
the retention interval, tretention. The average
time to identify the probe (tidentify) is
determined by Equation 35. Figure
10 shows
that with a value of ![]() prime = 1.2 sec, this model nicely
accounts for the serial position effects for various retention times.
prime = 1.2 sec, this model nicely
accounts for the serial position effects for various retention times.
|
|
Some experiments show that the average response to positive probes is
slightly faster than for negative probes (Burrows and Okada, 1971![]() ; Corballis et al.,
1972
; Corballis et al.,
1972![]() ). This feature can be
explained by repetition priming as well: only positive probes are
primed and hence have a faster RT. Figure 12 shows
how the adapting theta model captures this effect when a
500 msec retention interval is used. The RT for positive items
is ~60-70 msec faster than for negative items. From Figure 12 it can
also be seen that the model predicts that the slope for positive
items is 50% higher than the slope for negative items. According to
our model this is a direct consequence of the priming effect
resulting in faster RTs for positive items late is the list than
items earlier in the list. This prediction is consistent with some
experimental data in which fast presentation rates and short
retention intervals were applied. Corballis et al. (1972)
). This feature can be
explained by repetition priming as well: only positive probes are
primed and hence have a faster RT. Figure 12 shows
how the adapting theta model captures this effect when a
500 msec retention interval is used. The RT for positive items
is ~60-70 msec faster than for negative items. From Figure 12 it can
also be seen that the model predicts that the slope for positive
items is 50% higher than the slope for negative items. According to
our model this is a direct consequence of the priming effect
resulting in faster RTs for positive items late is the list than
items earlier in the list. This prediction is consistent with some
experimental data in which fast presentation rates and short
retention intervals were applied. Corballis et al. (1972)![]() found that positive
probes had 49% higher slopes than negative probes. Burrows and
Okada (1971)
found that positive
probes had 49% higher slopes than negative probes. Burrows and
Okada (1971)![]() found the value to be
18%. Many factors can contribute to the differences in the ratios,
such as presentation rate and training of the subjects.
found the value to be
18%. Many factors can contribute to the differences in the ratios,
such as presentation rate and training of the subjects.
|
| |
DISCUSSION |
|---|
Two oscillatory buffer models explain the RT distributions
We have found two models of a multiplexing buffer that can account
quantitatively for the RT distributions of the Sternberg paradigm.
Retrieval in these models is based on exhaustive serial search. The
models fit both the moments of the RT distributions measured by
Sternberg (1964)![]() and the actual
distributions measured by Ashby et al. (1993)
and the actual
distributions measured by Ashby et al. (1993)![]() . They can account for
the changes in these distributions with memory load and can be
applied to different subjects without having to assume differences in
fundamental oscillatory frequencies. The two models differ with
regard to theta adaptation and phase reset. In the first model
(adapting theta) the theta period varies with the number of items in
STM, but there is no reset of the oscillations when the probe
arrives. In the second model, the theta period is constant, but the
oscillation is phase-reset by the probe. We later discuss how these
assumptions can be tested.
. They can account for
the changes in these distributions with memory load and can be
applied to different subjects without having to assume differences in
fundamental oscillatory frequencies. The two models differ with
regard to theta adaptation and phase reset. In the first model
(adapting theta) the theta period varies with the number of items in
STM, but there is no reset of the oscillations when the probe
arrives. In the second model, the theta period is constant, but the
oscillation is phase-reset by the probe. We later discuss how these
assumptions can be tested.
Table 1 summarizes
the fitted values for the two models. With respect to the gamma frequency the
two models give values in the same range (46-59 Hz). These values are
in good agreement with experimentally observed data (Galambos et al.,
1981![]() ; Pantev et
al., 1991
; Pantev et
al., 1991![]() ; Joliot et al., 1994
; Joliot et al., 1994![]() ; Singer and Gray, 1995
; Singer and Gray, 1995![]() ; Tallon-Baudry
et al., 1997
; Tallon-Baudry
et al., 1997![]() , 1998
, 1998![]() ). In the adapting theta
model, slow-wave frequency depends on S and varies from 6 to
10 Hz, i.e., covering both the defined theta and alpha bands.
Note that both the Sternberg and Ashby data sets give rise to very
similar values. The reset model does not strongly constrain the value
of the theta frequency and allows frequencies in the interval from
4 to 7 Hz.
). In the adapting theta
model, slow-wave frequency depends on S and varies from 6 to
10 Hz, i.e., covering both the defined theta and alpha bands.
Note that both the Sternberg and Ashby data sets give rise to very
similar values. The reset model does not strongly constrain the value
of the theta frequency and allows frequencies in the interval from
4 to 7 Hz.
|
A key feature of the data that determines the value of gamma frequency is the
systematic changes in the rising edge of the cumulative response time
distribution with increasing S (Fig. 3). This is
the closest psychophysics comes to direct detection of gamma
frequency. However, an important conclusion of our work is that
deriving gamma from the data requires a full model. We originally
thought that the Sternberg slope (average increase in reaction time
per item) might directly correspond to the gamma period (Lisman and
Idiart, 1995![]() ). However, the models
presented here show the correspondence is only approximate. This is
because slope measurements are based on average RT, but this average
is determined not only by T
). However, the models
presented here show the correspondence is only approximate. This is
because slope measurements are based on average RT, but this average
is determined not only by T![]() but also the wait
time and skipping (Eqs. 13 and 27).
Consequently, the slope is ~1.5-2 higher than the gamma
period.
but also the wait
time and skipping (Eqs. 13 and 27).
Consequently, the slope is ~1.5-2 higher than the gamma
period.
The rising edge of the cumulative response distributions of a task related to
the Sternberg paradigm, the speed-accuracy trade-off (SAT) (McElree
and Dosher, 1989![]() ), does not have a
latency depending on S, whereas the Sternberg task does (Fig. 3). The SAT
data have been taken as an argument against serial scanning. However,
the SAT methodology is different from conventional recognition
memory paradigms in ways we believe limit the conclusions that can
be drawn. In this test, the subject is urged to respond at some
fixed time after the presentation of the test item by a signal to
respond. The presence of this signal and its processing introduce
processing problems not present in the Sternberg paradigm. Second,
although the signal to respond is given at a precise time, the
subsequent time to respond is not precise. This could be enforced by
only considering responses given with a precise latency but is
not. Because of this ambiguity, the method may not be able to
resolve small relevant delays on the order of
30 msec.
), does not have a
latency depending on S, whereas the Sternberg task does (Fig. 3). The SAT
data have been taken as an argument against serial scanning. However,
the SAT methodology is different from conventional recognition
memory paradigms in ways we believe limit the conclusions that can
be drawn. In this test, the subject is urged to respond at some
fixed time after the presentation of the test item by a signal to
respond. The presence of this signal and its processing introduce
processing problems not present in the Sternberg paradigm. Second,
although the signal to respond is given at a precise time, the
subsequent time to respond is not precise. This could be enforced by
only considering responses given with a precise latency but is
not. Because of this ambiguity, the method may not be able to
resolve small relevant delays on the order of
30 msec.
Several other models have been proposed that can account for the main
features of the RT distribution and the serial position effects.
Cavanagh (1976)![]() has investigated trace
strength models and holographic models, which both accounted for the
increase in RT with S and serial position effects of the Sternberg
paradigm. Ratcliff (1978)
has investigated trace
strength models and holographic models, which both accounted for the
increase in RT with S and serial position effects of the Sternberg
paradigm. Ratcliff (1978)![]() and Hockley and Murdock
(1987)
and Hockley and Murdock
(1987)![]() suggested decision
type models, which also successfully accounted for the RT
distributions and serial position effects. However, none of these
theories has been implemented in a physiologically realistic
way.
suggested decision
type models, which also successfully accounted for the RT
distributions and serial position effects. However, none of these
theories has been implemented in a physiologically realistic
way.
Possible rationale for exhaustive search
Sternberg concluded that memory search was exhaustive because RT depended
similarly on S for positive probes as for negative probes (for which
search is necessarily exhaustive). Because it would seem more
efficient for the motor response to begin as soon as a positive match
occurred (i.e., nonexhaustive search), some have argued that
exhaustive search is implausible. Our oscillatory model, however,
provides a plausible explanation for exhaustive search. All that
needs to be assumed is that initiation of the motor response can only
occur at the trough of the theta cycle. There are several examples in
the literature of the importance of theta phase for information
processing (Pavlides et al., 1988![]() ; O'Keefe and
Recce, 1993
; O'Keefe and
Recce, 1993![]() ; Nicolelis et al.,
1995
; Nicolelis et al.,
1995![]() ; Huerta and Lisman,
1996
; Huerta and Lisman,
1996![]() ).
).
Physiological tests for distinguishing between the models
The adapting theta model can be tested by analyzing EEG,
magnetoencephalography (MEG) and/or intracranial recordings on subjects
performing the Sternberg task. Results from imaging studies suggest
that prefrontal and parietal cortex are involved in the active
maintenance of STM (Shallice and Vallar, 1990![]() ; Cohen et al., 1997a
; Cohen et al., 1997a![]() ,b
,b![]() ; Jonides et
al., 1998
; Jonides et
al., 1998![]() ). We therefore expect to
observe the predicted changes in theta and gamma oscillations in
these areas. If the model is correct, the slow-wave oscillation
during the retention period should systematically decrease in
frequency with higher memory loads. Oscillations in the theta band
have been identified in humans performing STM tasks using both EEG
and MEG recordings (Gundel and Wilson, 1992
). We therefore expect to
observe the predicted changes in theta and gamma oscillations in
these areas. If the model is correct, the slow-wave oscillation
during the retention period should systematically decrease in
frequency with higher memory loads. Oscillations in the theta band
have been identified in humans performing STM tasks using both EEG
and MEG recordings (Gundel and Wilson, 1992![]() ; Mecklinger et al.,
1992
; Mecklinger et al.,
1992![]() ; Gevins et al.,
1997
; Gevins et al.,
1997![]() ; Klimesch et al., 1997
; Klimesch et al., 1997![]() ; Sarnthein et al.,
1998
; Sarnthein et al.,
1998![]() ). The band in
which theta oscillations have been observed is sufficiently broad to
allow the predicted adaptation with memory loads, but whether these
variations are related to memory load remains to the
tested.
). The band in
which theta oscillations have been observed is sufficiently broad to
allow the predicted adaptation with memory loads, but whether these
variations are related to memory load remains to the
tested.
The two models make different predictions about the effect of S on overall
neuronal firing and thus on the signals detected by brain-imaging
methods. In the reset model, the fraction of the theta period being
occupied by active memory representations increases with
S. Consequently, the number of activated neurons per theta cycle
will increase linearly with S (Fig. 13). In
contrast, the adapting theta model predicts a sublinear increase with
S (Fig. 13). These
predictions may be relevant in interpreting the data of Cohen et al.
(1997a![]() ,b
,b![]() ), which showed that
memory load (S) increases functional MRI signals in prefrontal
cortex, parietal areas, and Broca's area.
), which showed that
memory load (S) increases functional MRI signals in prefrontal
cortex, parietal areas, and Broca's area.
|
Examination of the load dependence of EEG amplitude may provide another way
of distinguishing the models. The factors controlling the amplitude
of EEG are unclear, but it seems plausible that amplitude would vary
with the number of neurons that fire within an oscillatory cycle.
Hence one might expect the theta amplitude to increases with
S. A study by Gevins et al. (1997)![]() points in
this direction: in an n-back task a higher power of
frontal-midline theta was observed for
n = 3 than for n = 1.
points in
this direction: in an n-back task a higher power of
frontal-midline theta was observed for
n = 3 than for n = 1.
A critical distinction between the adapting theta and reset models may be
made by studying the reset of the slow-wave oscillations after the
arrival of the probe. When S is small, there will be a fairly large
period during which there will be no cells firing. If the end of item
identification occurs during this period, the phase of oscillation
will be reset, and the resulting waveforms will be synchronized with
the probe onset. Although there will also be a less synchronized
component (if identification occurs during firing), the synchronous
component will be identifiable as an oscillation in the averaged EEG,
the evoked potential. Such a signal would not be generated if the
adapting theta model is correct. Several groups (Rahn and Basar,
1993a![]() ,b
,b![]() ; Brandt, 1997
; Brandt, 1997![]() ) have
reported components in the
) have
reported components in the ![]() range of averaged EEG
traces after simple stimuli, suggesting reset of the slow-wave
oscillations.
range of averaged EEG
traces after simple stimuli, suggesting reset of the slow-wave
oscillations.
Short-term repetition priming can account for serial position effects
Serial position effects have been used as an argument against serial
scanning. However, if the time for encoding of the probe can be
primed by previous exposure, our model can account quantitatively for
the serial position effect and retain the idea of serial scanning.
The decay of priming with ![]() = 1.2 sec
explains why the serial position effect becomes smaller for longer
retention intervals. Furthermore, priming explains why reaction times
are shorter for positive than negative probes, and why the RT slope
(increase in RT with S) is slightly steeper for positive than for
negative probes (Fig. 12).
Short-term repetition priming with a duration of a few seconds has
been observed in other psychophysical tests not necessarily related
to memory paradigms (Bertelson and Renkin, 1966
= 1.2 sec
explains why the serial position effect becomes smaller for longer
retention intervals. Furthermore, priming explains why reaction times
are shorter for positive than negative probes, and why the RT slope
(increase in RT with S) is slightly steeper for positive than for
negative probes (Fig. 12).
Short-term repetition priming with a duration of a few seconds has
been observed in other psychophysical tests not necessarily related
to memory paradigms (Bertelson and Renkin, 1966![]() ; Posner and Keele,
1967
; Posner and Keele,
1967![]() ; Smith et al., 1973
; Smith et al., 1973![]() ; McKone, 1995
; McKone, 1995![]() ). Monsell
(1978)
). Monsell
(1978)![]() showed that if an item
has been used as a negative probe in the previous trial, the response
time increases in the subsequent trial if the same item is used as a
positive probe. This finding has been used to argue against priming
as an explanation for the serial position effect. However, this
effect occurs over 10-15 sec, whereas repetition priming decays in a
few seconds; hence different mechanisms may be involved.
showed that if an item
has been used as a negative probe in the previous trial, the response
time increases in the subsequent trial if the same item is used as a
positive probe. This finding has been used to argue against priming
as an explanation for the serial position effect. However, this
effect occurs over 10-15 sec, whereas repetition priming decays in a
few seconds; hence different mechanisms may be involved.
Our proposal that priming of the encoding of the probe accounts for serial position effects (Fig. 10) leads to further predictions within the context of the reset model. A reset of the theta cycle follows the arrival of the probe. This reset will occur earlier for probes matching items late in the list compared with items early in the list. It should thus be interesting to look for the effect of serial position on the latency of evoked potentials.
In conclusion, we have found that a physiologically realistic model of serial memory search can account quantitatively for a large body of the data on STM. Furthermore, we have been able to counter some of the major objections to exhaustive serial search. Although it is certainly true that brain computations can occur in parallel, our results suggest that there may also be an important role for serial processing.
| |
FOOTNOTES |
|---|
Received June 9, 1998; revised Sept. 25, 1998; accepted October 1, 1998.
This work was supported by National Science Foundation Grant IBN-9723466 and
the Alfred P. Sloan Foundation. We gratefully acknowledge the
support from the W. M. Keck Foundation. We thank Michael Kahana
(Brandeis University) and Saul Sternberg (University of Pennsylvania)
for many helpful discussions. Saul Sternberg has kindly provided us
with his data on the moments of the RT distributions (Sternberg,
1964![]() ), and Greg Ashby
(University of California, Santa Barbara) and Jerry Balakrishnan
(Purdue University) have provided us with the full data set of the RT
distributions (Ashby et al., 1993
), and Greg Ashby
(University of California, Santa Barbara) and Jerry Balakrishnan
(Purdue University) have provided us with the full data set of the RT
distributions (Ashby et al., 1993![]() ).
).
Correspondence should be addressed to Dr. John E. Lisman, Volen Center for Complex Systems, Brandeis University, Waltham, MA 02243.
| |
APPENDIX |
|---|
Derivation of RT distribution for model I
In the first model the theta period (T| (2) |
| (3) |
| (4) |
| (5) |
| (6) |
| (7) |
| (8) |
| (9) |
| (10) |
| (11) |
| (12) |
| (13) |
| (14) |
| (15) |
| (16) |
| (17) |
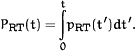 |
(18) |
| (19) |
Derivative of RT distribution for model II
In this model the period of the slow-wave oscillation (T| (20) |
| (21) |
| (22) |
| (23) |
| (24) |
| (25) |
| (26) |
| (27) |
| (28) |
| (29) |
| (30) |
| (31) |
Serial position
The time to identify a positive probe is shortened (primed) by the recent introduction of the equivalent item during presentation of the list. The time between the presentation of item i and the probe is given by:| (32) |
| (33) |
| (34) |
| (35) |
| (36) |
| (37) |
| |
REFERENCES |
|---|
.gif) -band activity induced by a visual search task in humans. J
Neurosci 17:722-734
-band activity induced by a visual search task in humans. J
Neurosci 17:722-734.gif) -band activity during the delay of a visual short-term memory
task in humans. J Neurosci 18:4244-4254
-band activity during the delay of a visual short-term memory
task in humans. J Neurosci 18:4244-4254
This article has been cited by other articles: (Search Google Scholar for Other Citing Articles)
 |
P. B. Sederberg, M. J. Kahana, M. W. Howard, E. J. Donner, and J. R. Madsen Theta and Gamma Oscillations during Encoding Predict Subsequent Recall J. Neurosci., November 26, 2003; 23(34): 10809 - 10814. [Abstract] [Full Text] [PDF] |
||||
|
| |||||
.gif) |
M. W. Howard, D. S. Rizzuto, J. B. Caplan, J. R. Madsen, J. Lisman, R. Aschenbrenner-Scheibe, A. Schulze-Bonhage, and M. J. Kahana Gamma Oscillations Correlate with Working Memory Load in Humans Cereb Cortex, December 1, 2003; 13(12): 1369 - 1374. [Abstract] [Full Text] [PDF] |
||||
|
| |||||
.gif) |
N. Sato and Y. Yamaguchi Memory Encoding by Theta Phase Precession in the Hippocampal Network Neural Comput., October 1, 2003; 15(10): 2379 - 2397. [Abstract] [Full Text] [PDF] |
||||
|
| |||||
.gif) |
D. S. Rizzuto, J. R. Madsen, E. B. Bromfield, A. Schulze-Bonhage, D. Seelig, R. Aschenbrenner-Scheibe, and M. J. Kahana Reset of human neocortical oscillations during a working memory task PNAS, June 24, 2003; 100(13): 7931 - 7936. [Abstract] [Full Text] [PDF] |
||||
|
| |||||
.gif) |
O. Jensen, J. Gelfand, J. Kounios, and J. E. Lisman Oscillations in the Alpha Band (9-12 Hz) Increase with Memory Load during Retention in a Short-term Memory Task Cereb Cortex, August 1, 2002; 12(8): 877 - 882. [Abstract] [Full Text] [PDF] |
||||
|
| |||||
.gif) |
L. Cornette, P. Dupont, E. Salmon, and G. A. Orban The Neural Substrate of Orientation Working Memory J. Cogn. Neurosci., August 1, 2001; 13(6): 813 - 828. [Abstract] [Full Text] [PDF] |
||||
|
| |||||
.gif) |
J. B. Caplan, J. R. Madsen, S. Raghavachari, and M. J. Kahana Distinct Patterns of Brain Oscillations Underlie Two Basic Parameters of Human Maze Learning J Neurophysiol, July 1, 2001; 86(1): 368 - 380. [Abstract] [Full Text] [PDF] |
||||
|
| |||||
 |
S. Raghavachari, M. J. Kahana, D. S. Rizzuto, J. B. Caplan, M. P. Kirschen, B. Bourgeois, J. R. Madsen, and J. E. Lisman Gating of Human Theta Oscillations by a Working Memory Task J. Neurosci., May 1, 2001; 21(9): 3175 - 3183. [Abstract] [Full Text] |
||||
|
| |||||
.gif) |
C. D. Tesche and J. Karhu Theta oscillations index human hippocampal activation during a working memory task PNAS, January 18, 2000; 97(2): 919 - 924. [Abstract] [Full Text] [PDF] |
||||
|
| |||||
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| HOME | HELP | FEEDBACK | SUBSCRIPTIONS | ARCHIVE | SEARCH | TABLE OF CONTENTS |